Salut les internautes
Aujourd’hui, je vous introduis à un concept clé en algorithmique: la complexité. Vous avez peut-être déjà entendu de complexité pour comparer des algorithmes qui résolvent le même problème. Dans ce court billet, je vais vous donner quelques clés permettant de comprendre ce qu’est la complexité et de la calculer. Pour comprendre ce billet, il vous faudra quelques notions de maths.
Basic notions of mathematics
Pour comprendre cet article, il vous faudra des bases en logique. D’abord, le symbole ![]() signifie “il existe… tel que”. Ce symbole
signifie “il existe… tel que”. Ce symbole ![]() signifie “pour tout”. Ce symbole
signifie “pour tout”. Ce symbole ![]() signifie “in”.
signifie “in”. ![]() est l’ensemble de tous les nombres naturels. Ainsi, par exemple
est l’ensemble de tous les nombres naturels. Ainsi, par exemple ![]() ou
ou ![]() signifie que pour tous
signifie que pour tous ![]() , nombre naturel, il y a
, nombre naturel, il y a ![]() , également nombre naturel tel que
, également nombre naturel tel que ![]() ou
ou ![]() .
.
Une des fonctions courantes en informatique est le logarithm. Dans ce billet, on se référera au logarithme comme log, et si ce n’est pas précisé, la base du logarithme pourra être n’importe quel entier.
Une fonction est définie par son domaine. ![]() signifie que
signifie que ![]() prend un élément de l’ensemble
prend un élément de l’ensemble ![]() et retourne un élément de l’ensemble
et retourne un élément de l’ensemble ![]() . La notation
. La notation ![]() donne une définition explicite.
donne une définition explicite.
Défintions
Fondamentalement, la complexité correspond au nombre d’opérations de base dont l’algorithme a besoin pour renvoyer le résultat. Dans ce calcul, nous ne regardons généralement pas le nombre précis d’opérations, mais plutôt le type de fonction utilisé. La complexité est généralement exprimée en fonction de certains paramètres ![]() . Ce paramètre est directement lié au problème. Lorsque le but est de commander un tableau,
. Ce paramètre est directement lié au problème. Lorsque le but est de commander un tableau, ![]() sera généralement la taille de ce tableau. Lorsque le but est de trouver un chemin dans un graphe,
sera généralement la taille de ce tableau. Lorsque le but est de trouver un chemin dans un graphe, ![]() sera le nombre de nœuds de ce graphe. Supposons maintenant que votre algorithme trie un tableau en
sera le nombre de nœuds de ce graphe. Supposons maintenant que votre algorithme trie un tableau en ![]() . Supposons maintenant qu’un autre algorithme trie le même tableau dans
. Supposons maintenant qu’un autre algorithme trie le même tableau dans ![]() . Dans ce cas, le deuxième algorithme sera plus efficace que le premier en ce qui concerne
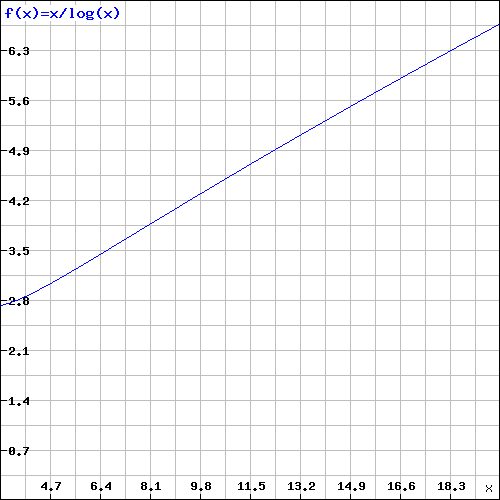
. Dans ce cas, le deuxième algorithme sera plus efficace que le premier en ce qui concerne ![]() . La courbe de cette fonction est:
. La courbe de cette fonction est:
Comme vous pouvez le voir, pour n assez grand, le second algorithme sera plus efficace que le premier. Puisque nous comparons les “ordres” des fonctions, la complexité est généralement exprimée en ![]() ,
, ![]() ou en
ou en ![]() . Ces trois fonctions sont cependant un peu différentes.
. Ces trois fonctions sont cependant un peu différentes.
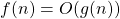 est appelée la “borne supérieure”. Cela signifie qu’il existe une constante C telle que pour n assez grand,
est appelée la “borne supérieure”. Cela signifie qu’il existe une constante C telle que pour n assez grand, 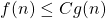
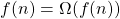 est appelée la “borne inférieure”. Cela signifie qu’il existe une constante C telle que pour n assez grand,
est appelée la “borne inférieure”. Cela signifie qu’il existe une constante C telle que pour n assez grand, 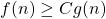
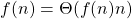 est appelé l’ “équivalence asymptotique”. Cela signifie qu’il existe deux constantes C et D telles que pour n assez grand,
est appelé l’ “équivalence asymptotique”. Cela signifie qu’il existe deux constantes C et D telles que pour n assez grand, 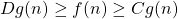
Pour résumer, ![]() signifie que g croît plus vite que f (ou aussi vite que f),
signifie que g croît plus vite que f (ou aussi vite que f), ![]() signifie que g croît plus lentement que f (ou aussi vite que f) et
signifie que g croît plus lentement que f (ou aussi vite que f) et ![]() signifie que g croît aussi vite que f. Par exemple pour la fonction:
signifie que g croît aussi vite que f. Par exemple pour la fonction: ![]() nous pouvons écrire f (n) = O (n²).
nous pouvons écrire f (n) = O (n²).
Récursion
L’une des techniques algorithmiques les plus usitées consiste à résoudre une partie d’un problème et à s’appliquer ensuite aux sous-parties résolues. Un bon exemple d’un tel mécanisme est la détermination de la séquence la plus longue de caractères similaires dans une chaîne (par exemple, la séquence la plus longue dans baababbbcccbbabbbbbca est bbbbb). Pour ce faire, nous prenons le caractère central de la chaîne, qui sera appelé le “pivot”. On retrouve alors la séquence la plus longue du même caractère dans la première moitié du tableau, avant le pivot, et la séquence la plus longue dans la seconde moitié du tableau, après le pivot. Enfin, nous recherchons dans l’ensemble du tableau la séquence la plus longue du tableau contenant le pivot. Pour trouver la séquence la plus longue contenant le pivot, nous parcourons la chaîne du pivot vers l’arrière et vers l’avant jusqu’à ce que nous trouvions un caractère différent du pivot. Nous parcourons au maximum n caractères, où n est la longueur de la chaîne. L’algorithme est le suivant:
LongestSequence(string, start, end): if start=end return null seq ← null pivot ← string[start/2+end/2] i ← pivot while(i≠start and string[i]=pivot): seq.add(string[i]) i ← i-1 seq.add(pivot) i ← pivot while(i≠end and string[i]=pivot): seq.add(string[i]) i ← i+1 left ← LongestSequence(string, start, pivot-1) right ← LongestSequence(string, pivot+1, end) if(length(left)>length(right) and length(left)>length(seq)) return left else if (length(right)>length(seq)) return right else return seq
Cet exemple montre comment fonctionne la récursion. Cette méthode (qu’on appelle aussi diviser pour régner) est très pratique. L’un des problèmes de récursion est qu’il est assez difficile de calculer le nombre d’opérations nécessaires pour terminer l’algorithme.
Complexité d’un algorithme récursif
Il existe trois méthodes pour calculer la complexité d’un algorithme récursif :
- Arbres de récursion
- Méthode de substitution
- Master theorem
Arbres de récursion
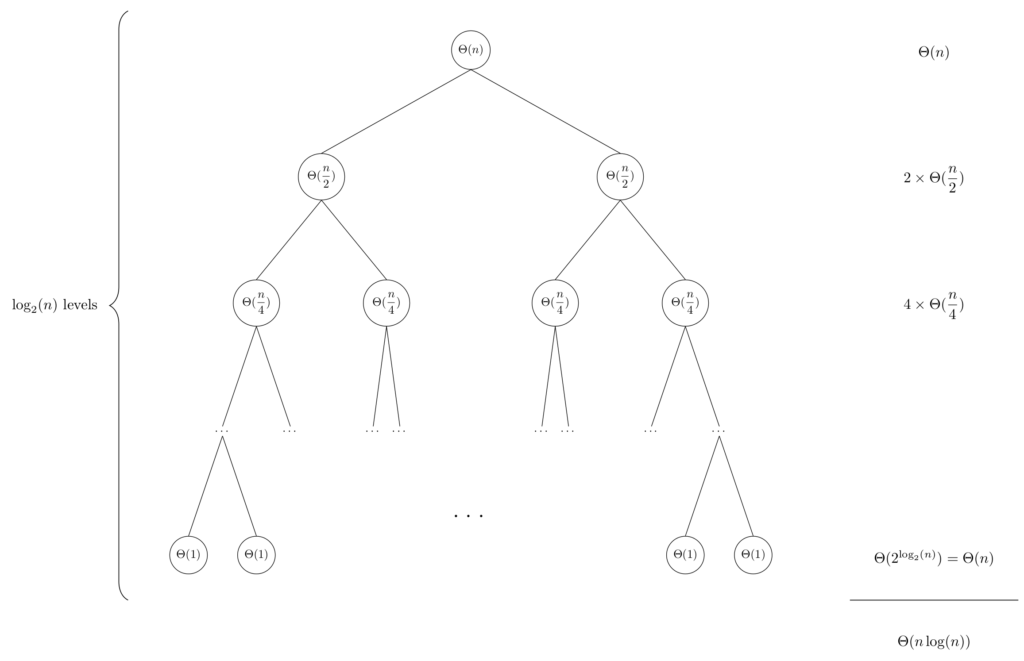
Les arbres de récursion sont un outil très utile pour étudier la complexité des algorithmes récursifs. Chaque nœud de l’arbre représente le nombre d’opérations effectuées à ce niveau. Les enfants d’un nœud représentent les divisions dans la méthode de récursion. La figure ci-dessous représente l’arbre de récursivité de notre problème de séquence:
Les arbres de récursion sont souvent utilisés pour obtenir une incitation qui sera confirmée en utilisant la méthode de substitution. Cependant, il est possible de les utiliser comme preuve. Dans ce cas, il est nécessaire d’être très strict sur la manière de traiter le problème. Pour voir instictivement pourquoi notre problème s’exécute en ![]() , regardons la figure. La complexité est
, regardons la figure. La complexité est
![]() .
.
La méthode de substitution
Pour utiliser la méthode de substitution, il est nécessaire d’avoir une compréhension instinctive de la complexité de l’algorithme. Une fois que vous en avez une, l’idée est de remplacer l’expression de ![]() par sa valeur supposée. Ainsi, par exemple, dans notre exemple précédent, si nous supposons
par sa valeur supposée. Ainsi, par exemple, dans notre exemple précédent, si nous supposons ![]() :
:![]()
![]()
![]()
![]()
![]() si
si ![]()
Le master theorem
Le master theorem est très utile dans de nombreux cas pour résoudre la complexité des algorithmes récursifs. L’énoncé de ce théorème est:
Supposons une récurrence de la forme:![]()
Alors:
- Si
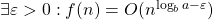 alors
alors 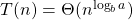 .
. - Si
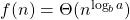 alors
alors 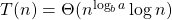
- Si
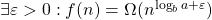 et
et 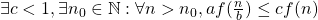 alors
alors 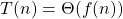 .
.
Dans notre exemple, nous avons ![]() et
et ![]() nous sommes dans le second cas. Ainsi,
nous sommes dans le second cas. Ainsi, ![]() .
.
Notez que ce théorème est très utile mais ne peut pas être utilisé tout le temps. En effet, il pourrait arriver que l’équation ne tombe dans aucun de ces cas à cause des ε: par exemple, f (n) peut être plus petit que ![]() mais il n’y a pas d’epsilon tel que
mais il n’y a pas d’epsilon tel que ![]() . Dans ce type de cas, il est nécessaire d’utiliser une autre des techniques présentées.
. Dans ce type de cas, il est nécessaire d’utiliser une autre des techniques présentées.
Voilà les internautes. On est loin, très loin d’avoir épuisé le sujet bien entendu, mais j’espère que ce petit billet vous aura plu. Il existe pleins de problématiques allant des classes de complexité aux manières de calculer la complexité d’un algorithme de manière plus précise via des méthodes plus particulières comme la complexité amortie. Nous en reparlerons dans de futurs billets, et si vous voulez en savoir plus, je vous recommande les chapitres 4, 17 et 34 du livre Algorithmique1. D’ici-là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver.
Cormen, T., Leiserson, C., Rivest, R., & Stein, C. (2010). Algorithmique. Cours, exercices et problèmes. Dunod, Paris,. ↩