Un grand merci à Karim El Mernissi pour sa relecture et ses précieux conseils !
Salut les internautes. Depuis le temps que j’en parle, je vais faire une petite intro au Monte Carlo Tree Search. Mais pour faire ça bien, je vais devoir commencer par les bases. Il faut que je parle de jeux, de leur résolution, et des méthodes heuristiques.
Evidemment, ça se fera pas en un seul billet, donc on va commencer par les jeux aujourd’hui. Donc pour rappel, MCTS c’est la méthode implémentée dans AlphaGo qui lui a récemment permis de battre les autres IA aux échecs, au Shogi et au Go.
Du coup, aujourd’hui, on va parler de cette catégorie de jeux, qu’on appelle les jeux combinatoires (vous pouvez aussi jeter un oeil sur Wikipedia). Les jeux combinatoires sont caractérisés par un ensemble d’éléments.
D’abord, ce sont des jeux à 2 joueurs. En général, ce sont des jeux symétriques (c’est à dire que les deux joueurs ont les mêmes coups disponibles), mais ce n’est pas obligatoire. Ce sont aussi des jeux où il n’y a pas de hasard.
Les joueurs savent quel est le but de chacun et connaissent l’historique des coups qui ont été joués ; on dit que les jeux combinatoires sont respectivement à information parfaite et complète. Deux contre-exemples : si vous avez déjà joué aux loups-garous, vous ne connaissez pas le type des autres joueurs, ni donc leur but.
A la bataille navale, la manière dont votre adversaire a placé ses bateaux est inconnue, vous n’avez donc pas les informations sur tout l’historique.
Enfin, on s’interdit (théoriquement) les égalités : on a donc un gagnant et un perdant. Il n’y a pas de situation où on a deux gagnants ou deux perdants. En pratique, il arrive qu’on accepté de telles égalités, par exemple aux échecs.
On dit que le jeu est à somme nulle : on associe une utilité à chaque joueur, généralement 1 au vainqueur et -1 au vaincu, la somme faisant 0. Il n’y a pas d’issue avec 2 gagnants ou 2 perdants.
L’avantage de ces jeux, c’est qu’on peut les représenter sous la forme d’un arbre. Pour la suite, je vais prendre un exemple de jeu simple: la somme à 5.
Voici les règles :
- On a deux joueurs, Droite et Gauche
- Gauche commence
- Un compteur est initialisé à 0
- A son tour, chaque joueur peut incrémenter le compteur de 1 ou 2
- Le premier qui atteint 5 a gagné.
C’est un jeu combinatoire très simple. On en retrouve toutes les caractéristiques : 2 joueurs, déterministe, information complète et parfaite, somme nulle, un gagnants et un perdant (pas de nul).
Pour ceux qui ne connaissent pas les arbres, très vite :
- un arbre c’est une structure de donnée ;
- il est composé de noeuds et d’arêtes (comme un graphe) ;
- on a un noeud tout en haut de l’arbre, appelé racine ;
- en-dessous, on trouve d’autres noeuds reliés à la racine par des arêtes. On dit que ces noeuds sont les “fils” de la racine. Ces noeuds peuvent eux-mêmes avoir des fils etc ;
- un noeud sans fils est nommé “feuille”.
Si on prend n’importe quel noeud, on peut le considérer comme la racine de l’arbre constitué de lui et de ses descendants. On parle de sous-arbres. et un exemple pour marquer les esprits : prenons votre arbre généalogique.
Vous êtes la racine de cet arbre. Au-dessous se trouvent vos parents (ces noeuds sont techniquement des noeuds fils du votre), leur parents sont leurs propres neouds fils etc.
Le sous-arbre dont votre père constitue la racine est l’ensemble de vos ascendants paternels.
Maintenant, on va représenter la somme à 5 sous la forme d’un arbre.
- l’arbre a pour racine l’état initial du jeu;
- chaque noeud correspond au résultat de l’actoin du joueur à qui c’est le tour.
- puisqu’un joueur a deux actions possibles au plus à chaque tour, chaque noeud a au plus 2 fils. Par exemple, la racine a pour fils la sitation où Gauche joue 1 et celle ou iel joue 2.
Voilà l’arbre complet:
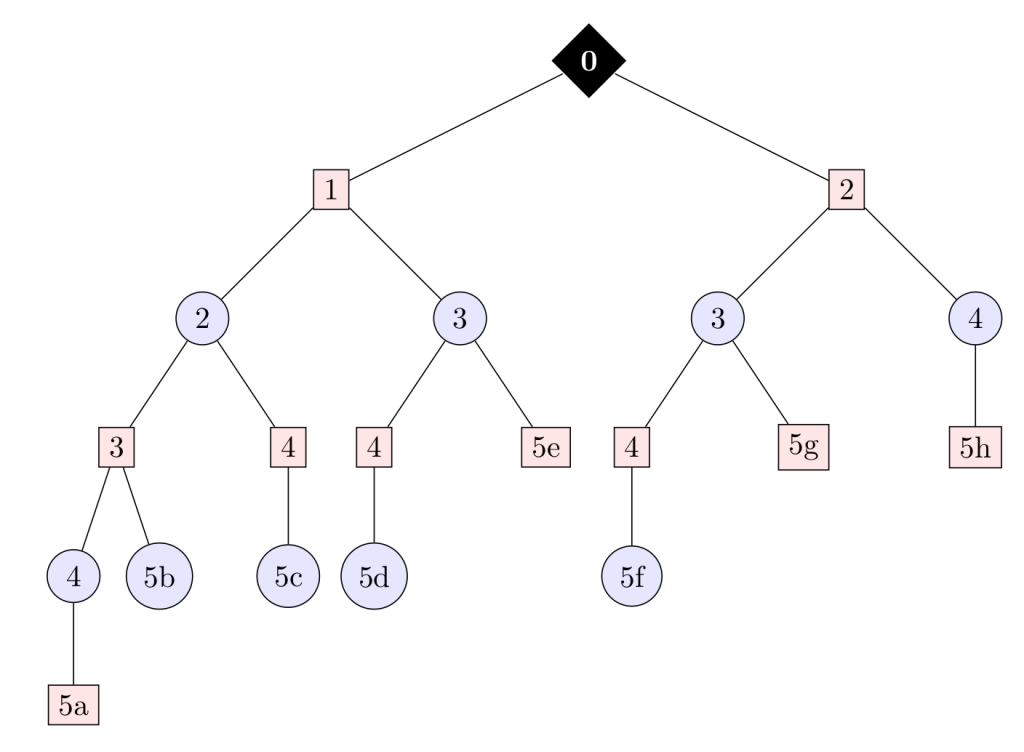
Il se finit toujours par un joueur qui joue 5 et donc gagne. Les situations finales sont étiquetées avec des lettres.
Les situations a, e, g et h ont pour vainqueur Gauche (score de Gauche : 1, score de Droite : -1; on écrit (1,-1)). Pour les situations b, c, d et f, c’est l’inverse : (-1,1). Cette représentation des jeux est appelée forme extensive
Voilà, c’est tout pour aujourd’hui. La prochaine fois, on parlera de résolution et d’heuristiques. D’ici là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver.




