Merci à Karim de m’avoir relu.
Salut les internautes ! Aujourd’hui, je continue ce que j’avais instancié en début de semaine, à savoir de la vulgarisation autour de l’intelligence artificielle, et plus précisément l’IA pour les jeux. Pour rappel, le but final est d’expliquer l’algo MCTS.
Pour rappel, dans le dernier épisode disponible ici, j’expliquais comment on pouvait représenter un jeu combinatoire comme les échecs ou le go sous forme d’arbre, ou forme extensive.
Une IA qui sait jouer au go ou aux échecs ne semble pas avoir de véritable plus-value. Elle ne va pas sauver de gens ou vous aider à surveiller votre maison. Pourtant, les jeux ont été le terrain de jeu de l’IA dès sa création.
On dit souvent des échecs qu’ils ont servi de “drosophile” aux chercheurs en IA. Il y a une grande part de vérité là-dedans. L’avantage des jeux est qu’ils rassemblent deux caractéristiques que l’on trouve rarement ensemble.
Ils sont à la fois conceptuellement simples et demandent le déploiement d’une grande complexité pour leur résolution. On l’a vu, ils sont représentables sous la forme d’arbres, mais leur combinatoire est telle qu’ils représentent un challenge.
C’est ainsi que pendant longtemps, on a considéré qu’il fallait nécessairement être intelligent pour gagner aux échecs face à un grand maître. Aujourd’hui, cette conception de l’intelligence est passée.
Il n’en reste pas moins que les jeux sont toujours intéressants. De par leur formalisme, ils permettent de s’abstraire des problèmes de modélisation du monde, tout en étant assez complexes pour que les résultats du domaine aient un intérêt.
Il existe deux manières de gagner un jeu. Aujourd’hui, nous allons nous intéresser à la première, c’est à dire le résoudre. Résoudre un jeu consiste à trouver la stratégie optimale pour le gagner. Il n’est pas toujours nécessaire d’en explorer tout l’arbre, mais pas loin.
L’exploration des possibilités est très longue, y compris pour des jeux relativement simples (e.g. les dames). Il existe deux manières de faire. On peut d’abord partir du bas de l’arbre et le remonter.
On détermine les positions gagnantes et perdantes, et on propage depuis le bas de l’arbre ces informations. Lorsqu’on propage, on suppose toujours que les joueurs jouent de manière optimale, c’est à dire qu’ils gagneront s’ils le peuvent.
Reprenons l’exemple de la somme à 5, dont je vous remets l’arbre. Lorsqu’on part de la solution 5a, où Gauche a gagné. le noeud juste au-dessus est un noeud de Droite. Or, au coup précédent, Droite aurait pu jouer 5b et gagner.
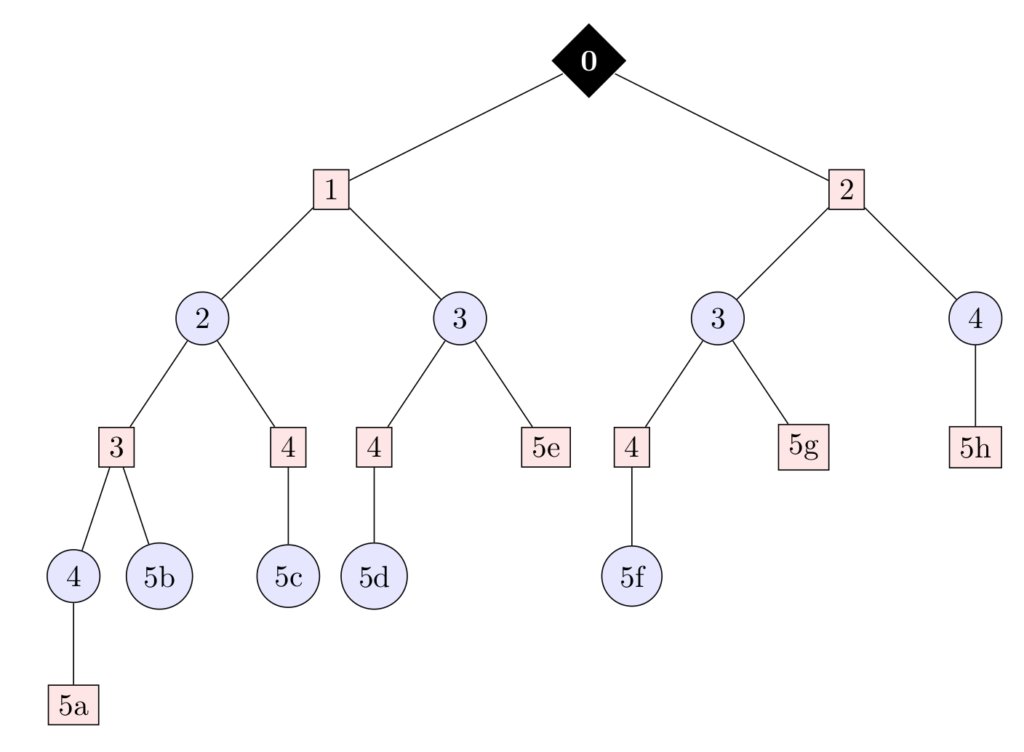
Supposer les agents parfaitement rationnels, c’est dire que Droite choisira la meilleure solution pour lui et jouera 5b et non 4. On peut donc dire que jouer le noeud au-dessus est perdant pour Gauche. Il est possible d’utiliser cette particularité pour ne pas explorer (ou “élaguer”) certaines branches de l’arbre. Par exemple, en supposant qu’on n’ait pas exploré le chemin 4 5a, mais uniquement 5b, on sait que Droite peut gagner à partir de 3.
Il est alors inutile de vérifier le second, puisque Droite est supposé parfaitement rationnel et qu’on suppose qu’il jouera le chemin qui l’amène de manière certaine à la victoire, c’est à dire 5b.
Dans l’autre sens, il est possible de partir du haut de l’arbre pour le réduire. Par exemple, la situation du jeu dans le cas Gauche : 1, Droite : 2, Gauche : 4 amène à la même situation que Gauche : 2, Droite : 3, Gauche : 4.
En effet, dans les deux cas, c’est à Droite de jouer et le compteur est à 4. Si on a résolu une des deux situations, l’autre se résout de la même manière. Il n’en reste pas moins que certains jeux sont insolubles.
Claude Shannon a estimé que la complexité des échecs (le nombre de partie possible) était de l’ordre de 10^120, c’est à dire plus que le nombre d’atomes de l’univers. Le go est encore plus grand.
Même en utilisant ces « trucs », il paraît peu probable que nous soyons un jour capables de résoudre un tel jeu. Il est alors nécessaire d’utiliser l’autre approche, c’est à dire trouver une stratégie qui soit bonne.
Il ne s’agit pas de la stratégie optimale, mais d’une stratégie qui est meilleure que toutes les autres. C’est ce qui a été fait par Deep Blue et AlphaGo.
Dans le prochain épisode, je vous parlerai d’heuristiques. D’ici là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver.