Salut les internautes. J’ai consacré il y a quelque temps un court billet à la définition d’un jeu en théorie des jeux, mais aujourd’hui, en va aller un peu plus dans le détail. Je vais redonner une définition d’un jeu (en français) et je vais développer un peu, en expliquant deux manières de représenter un jeu: sous sa forme extensive et sous sa forme normale.
Un jeu est un processus impliquant un nombre n de joueurs, A tout moment, le jeu est dans une position, et un ou plusieurs joueurs sont invités à agir conformément à des règles de manière à changer l’état du jeu. Selon les règles, le jeu se termine quand il est dans certains états, et pour chacun de ces états, chaque joueur reçoit un score.
Nous allons donner la définition d’une catégorie de jeux très étudiée: les jeux combinatoires. On y trouve le morpion, les dames, les échecs, le Go ou encore le Hex. Les jeux combinatoires sont des jeux séquentiels (les joueurs jouent les uns après les autres) à 2 joueurs. L’état du jeu, l’historique de ses états intérieurs ainsi que la fonction donnant le score des joueurs en fonction de l’état final du jeu sont connues (on dit que le jeu est à information parfaite et complète). La somme des scores des deux joueurs est égal à 0 (on dit que le jeu est à somme nulle). D’autre part, les transitions d’état du jeu ne dépendent que des décisions prises par les joueurs et n’impliquent pas de processus aléatoire (on dit que le jeu est déterministe). Ces jeux sont très communs, et ce sont les plus étudiés.
Avant de passer aux définitions des formes normale et extensive des jeux, je vais vous donner un contre exemple de chacun des termes ci-dessus:
- Pierre-feuille-ciseaux est un jeu simultané (et non séquentiel)
- La belote est un jeu à 4 joueurs
- La bataille navale est un jeu à information imparfaite, car on connaît pas tout l’historique du jeu (on ne sait pas où l’adversaire a placé ses bateaux)
- Les loups-garous de Thiercelieux (ou Mafia) est un jeu à information incomplète, car les personnages jouant les villageois ne connaissent pas le score des autres joueurs en fonction de la situation finale (victoire des loups garous vs des villageois)
- Le dilemme du prisonnier est un jeu à somme non nulle (si les prisonniers se taisent tous les deux, ils obtiennent un score total supérieur )à s’ils trahissent tous les deux).
- Le poker est un jeu non déterministe, puisqu’il utilise un processus aléatoire lors de la distribution des cartes.
Les définitions que je vais donner ci-dessous sont valables pour tous types de jeux. Il est aussi possible de définir les jeux en fonction de leur symétrie, selon que les joueurs ont le même rôle ou non. Pierre-feuille-ciseaux est symétrique, Les loups garous de Thiercelieux ne l’est pas.
La forme normale
La forme normale est une représentation des scores des différents joueurs sous forme d’un tableau, en fonction des actions entreprises par les joueurs. La forme normale est en général utilisée pour des jeux simples, qui demandent à chaque joueur de faire une unique action. Prenons l’exemple de pierre-feuille-ciseaux. Ce jeu est un jeu à somme nulle, dont la forme normale peut être représentée par:
| Joueur 1 | ||||
| pierre | feuille | ciseaux | ||
| Joueur 2 | pierre | (0,0) | (1,-1) | (-1,1) |
| feuille | (-1,1) | (0,0) | (1,-1) | |
| ciseaux | (1,-1) | (-1,1) | (0,0) |
Représentation du jeu de Pierre – Feuille – Ciseaux sous forme normale
Les scores sont placés dans le tableau selon le numéro du joueur: le joueur 1 d’abord, le joueur 2 ensuite. Il est possible de représenter des jeux plus complexe sous forme normale, mais cela devient vite compliqué car il faut expliciter toute les stratégies possibles des joueurs et le tableau devient rapidement illisible. L’avantage d’une telle représentation en revanche est d’identifier très vite si certaines stratégies sont « meilleures » que d’autres (on dit dans ce cas que les meilleures stratégies dominent les moins bonnes). Plus formellement pour un jeu à deux joueurs
Soit i un joueur, et s₁, s₂ deux stratégies pour ce joueur. Soit -i l’autre joueur. On note g la fonction de score (gᵢ(s, s’) le score de i sachant que i a choisi la stratégie s et -i la stratégie s’ et g₋ᵢ(s, s’) le score de -i dans cette même situation). Alors on dit que s₁ domine faiblement s₂ si et seulement si:
∀s: gᵢ(s₁,s)≥gᵢ(s₂,s)
Quel que soit la stratégie choisie par l’adversaire de l’agent, la stratégie 1 lui rapporte un meilleur score que la stratégie 2. On peut donner la définition de la domination stricte en reprenant la même définition et en remplaçant le symbole ≥ par un symbole >.
La forme extensive
Comme on l’a vu, la forme normale d’un jeu n’est pas très pratique pour représenter des jeux longs, car elle donne lieu à une colonne/ligne par stratégie possible de chaque joueur. Pour éviter des représentations peu pratiques, on représente en général les jeux impliquant plus d’un mouvement de l’un ou l’autre des agents sous une autre forme, la forme extensive. Cette manière de représenter un jeu consiste à créer un arbre, qui montre les possibles actions de chaque agent. Prenons un exemple. Supposons le jeu suivant: le jeu consiste prendre un compteur et à l’initialiser à 0. Chaque joueur, à son tour, peut incrémenter le compteur de 1 ou 2. Le jeu se termine quand un joueur arrive à 5 (ou plus), et le dernier joueur à avoir joué gagne. Représenter ce jeu sous forme normale est très compliqué. Il faudrait faire le déroulé de chaque partie et donner le score de chaque joueur dans chaque situation finale. En revanche, il est aisé de le représenter sous la forme d’un arbre. La figure ci-dessous donne l’exemple d’une telle représentation. Dans cette figure, chaque nœud de l’arbre représente l’action d’un joueur (le joueur i en bleu et le joueur -i en rouge). Le nombre sur le nœud représente l’action réalisée par le joueur (le nombre qu’il a annoncé) et les nombres entre parenthèse à la fin représentent le score pour chaque situation finale.
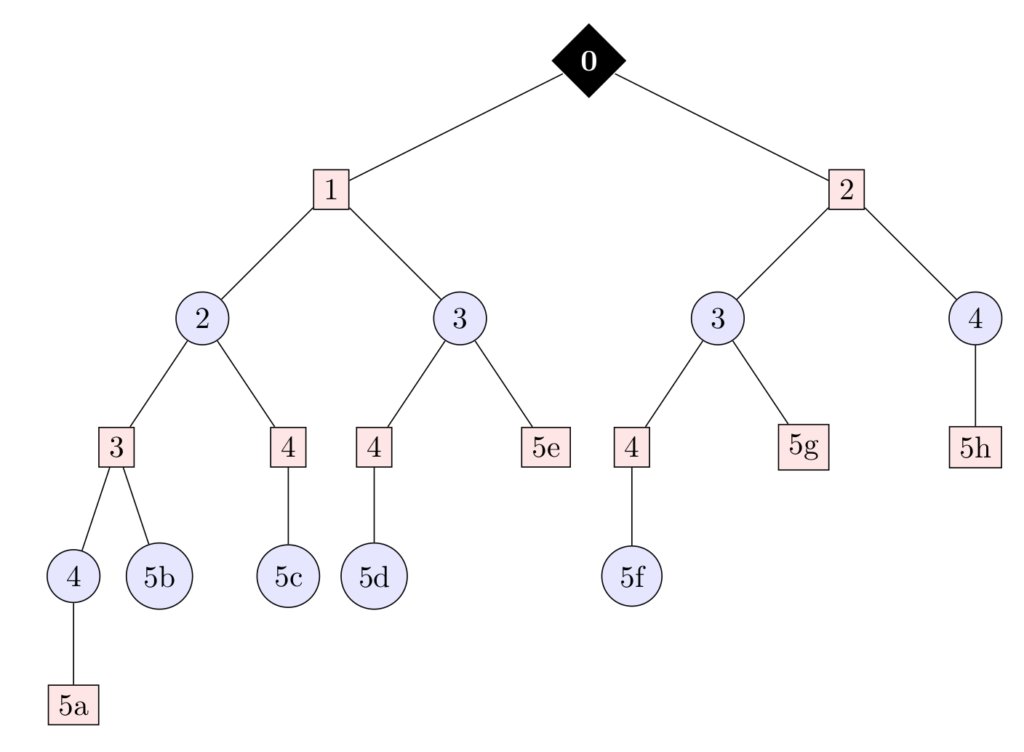
Représentation du jeu de somme à 5 sous forme extensive
Cette représentation du jeu est utilisée, notamment pour créer des intelligences artificielles, car elle rend évidente l’utilisation de techniques comme le maximin. Je vous expliquerai cette méthode dans un autre article dédié à cette technique prochainement. Avant de partir, vous trouverez en référence un ouvrage de Yoav Shoham et Kevin Leyton-Brown particulièrement bien écrit en anglais sur les domaines liés au SMA, avec de très bons chapitres sur la théorie des jeux. Il est accessible librement, et je ne saurais trop vous encourager à jeter un œil si vous souhaitez en savoir davantage. D’ici-là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver.