Salut les internautes. Dans notre dernier billet sur la théorie des jeux j’avais parlé de forme normale et de forme extensive et je vous avais dit que la forme normale était particulièrement utile pour détecter les stratégies dominantes. Je n’avais alors donné qu’une intuition de ce qu’est une stratégie. Dans ce billet, je vais revenir sur cet élément incontournable de la théorie des jeux.
Avant de me lancer dans le cœur du sujet, je tiens à préciser qu’il est possible de trouver plusieurs définitions pour le terme stratégie. J’en ai choisi une, qui me paraît adaptée, et qui répond surtout à mes futurs besoins: en effet, le but de cette série de billets est de glisser vers l’intelligence artificielle, et plus précisément vers les techniques d’IA pour les jeux. Certains définissent en particulier l’ensemble des stratégies comme l’ensemble des actions possibles dans un jeu donné. Je choisis volontairement une autre définition.
Formalisation
La première étape va consister à formaliser un peu ce que nous avons vu la dernière fois. On va considérer un jeu comme un automate. Un jeu est donc constitué d’un état, et pour chaque état d’un ensemble d’actions possibles. Ces actions peuvent être vues comme des transitions d’un état vers un autre. Vous êtes un peu perdu ? Pas d’inquiétude, on va prendre un exemple. Prenons l’exemple du Morpion, dont le plateau est partiellement rempli:
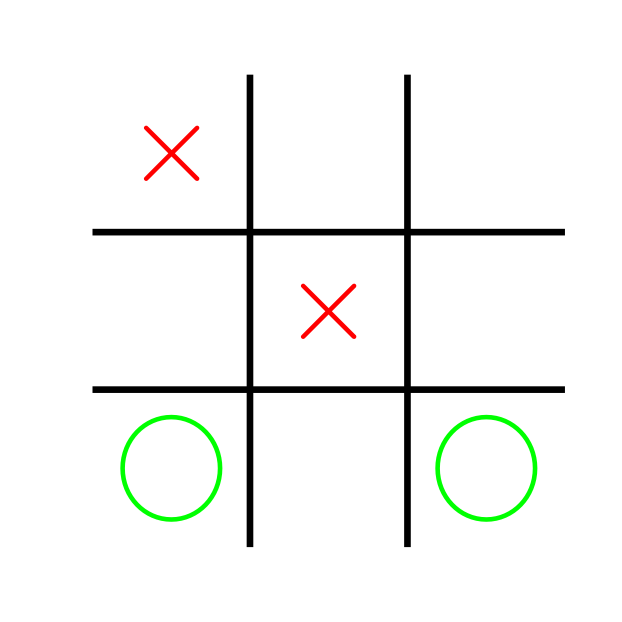
Ce plateau ne constitue pas, à lui tout seul, l’état du jeu. Il est en effet nécessaire d’ajouter une information: quel est le prochain joueur à jouer. Ici, on va supposer que c’est à Rouge de jouer. Au morpion, l’état du plateau et la désignation du joueur qui doit jouer constitue toutes les informations dont un joueur à besoin pour jouer (en particulier, l’ordre dans lequel les coups précédent ont été joués n’est pas important). Cela constitue donc un état du jeu. À partir de là, il est possible pour Rouge de jouer sur chaque case possible, menant à un nouvel état composé du plateau de jeu avec la croix rouge en plus, et du fait que c’est à Vert de jouer. Ces possibilités de jeu constituent les actions possible, que l’on peut voir comme les transitions entre les états du jeu. On peut donc représenter un jeu G comme:
G = (A,S,s₀,δ,F,ω)
où A est l’ensemble des actions possibles à tout moment dans le jeu (contenant le joueur et son action sur le plateau), S est l’ensemble des états du jeu, s₀ est l’état initial du jeu (qui définit notamment le plateau “vide” et le premier joueur), δ est une fonction (la fonction de transition) qui à un état s de S et une action a de A associe un nouvel état s’ de S si le mouvement est légal. F contient l’ensemble des états finaux, soit les états où un des joueurs est gagnants ou un état où aucun ne peut plus jouer1.
Enfin, ω est la fonction de score, qui à tout état de F associe un score pour chaque joueur.
Stratégies
Donnons désormais une définition de ce qu’est une stratégie. On définit une stratégie de comme une fonction σ qui à tout état s de S associe une action a de A. Comme la fonction de transition, cette fonction est partielle au sens où la stratégie ne prend en compte que les états où on peut jouer (et non les états finaux, ou les états où c’est à l’adversaire de jouer). Là encore, la définition peut paraître un peu barbare, nous allons donc l’illustrer par un exemple. On va choisir un jeu facile à expliciter, car en règle générale, l’explicitation de la stratégie demande l’explicitation de tous les états possibles. Pour éviter une explication trop longue, prenons le Black Jack simplifié:
Il s’agit d’un jeu à deux joueurs
- À chaque tour, chaque joueur peut tirer une carte ou non (on dit qu’il reste). Chaque carte a une valeur contenue entre 1 et 10. Lorsqu’il tire une carte, le joueur qui l’a tirée ajoute le score de cette carte à son propre score.
- Si le score d’un joueur dépasse 21, il perd.
- Si un joueur ne tire pas de carte, il ne peut plus en tirer, définitivement. Son adversaire peut alors en tirer autant qu’il le souhaite.
- Une fois que le second joueur est resté, le jeu se termine.
Un état du jeu est alors composé des indications suivantes: le joueur auquel c’est le tour de jouer, le score de chaque joueur, et si un des joueur est resté, et auquel cas, lequel. Un exemple de stratégie (appelons-la σ) dans ce cas est alors:
- Si mon adversaire est dans la partie, que mon score est inférieur au sien ou que mon score est inférieur à 16, je prends une carte,
- Si mon adversaire est resté, je prends une carte jusqu’à dépasser son score.
- Si mon adversaire n’est pas resté et que mon score est strictement supérieur à 16, je reste.
Cette stratégie couvre tous les cas possibles (ce qui est vérifiable par disjonction sur les états possibles du jeu) et associe bien à tout état du jeu une action légale du jeu (tirer une carte ou rester).
Dominance stratégique
Définissons maintenant plus clairement ce qu’est une stratégie dominante. On dit qu’une stratégie en domine une autre si elle est meilleure (si elle mène à un meilleur score pour son joueur) quelle que soit la stratégie de son adversaire. Prenons le cas du jeu décrit précédemment, et définissons la stratégie σ’ comme la stratégie σ si le score du joueur est inférieur ou égal à 20 et comme “tirer une carte” quand le score du joueur est égal à 21. Alors, dans tous les cas pour une partie du jeu:
- Soit on n’atteint pas un état où le joueur a un score de 21 et la stratégie σ’ est aussi bonne que la stratégie σ.
- Soit on atteint l’état où le joueur a un score de 21 et dans ce cas, tirer une carte l’amènera forcément à perdre.
La stratégie σ’ amène donc un score au mieux identique à σ, au pire elle perd là où σ aurait gagné ou au moins fait égalité à 21. On dit dans ce cas que σ domine σ’. Une stratégie est dite dominante si elle domine toutes les autres stratégies possibles.
Voilà les internautes. J’espère que ce billet un peu plus matheux ne vous aura pas trop perdu (si c’est le cas, faites-le moi savoir en commentaire). Je vous reviens dès que je peux avec la suite de cette série de billets sur la théorie des jeux. D’ici-là, renseignez-vous, réfléchissez et surtout, n’oubliez pas de rêver !
Ces cinq premiers éléments correspondent à la définition d’un automate cellulaire. Voir la page Wikipedia. ↩




